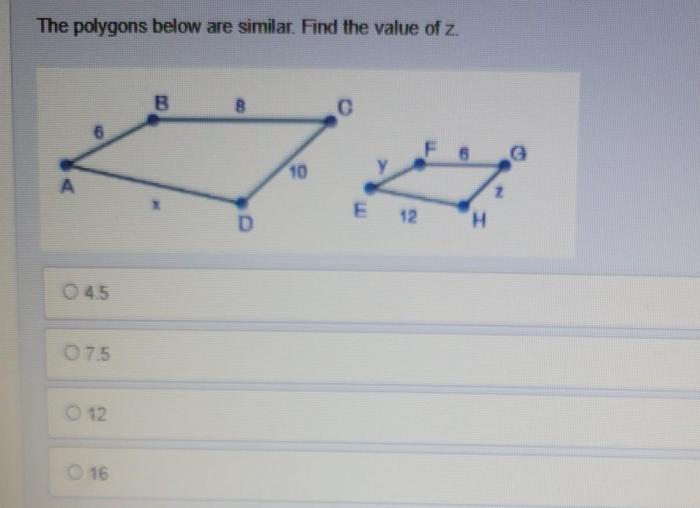
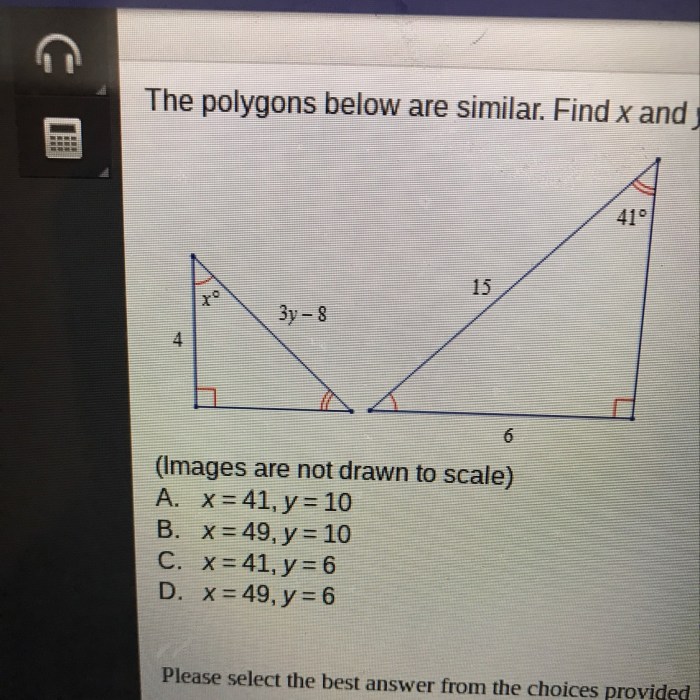
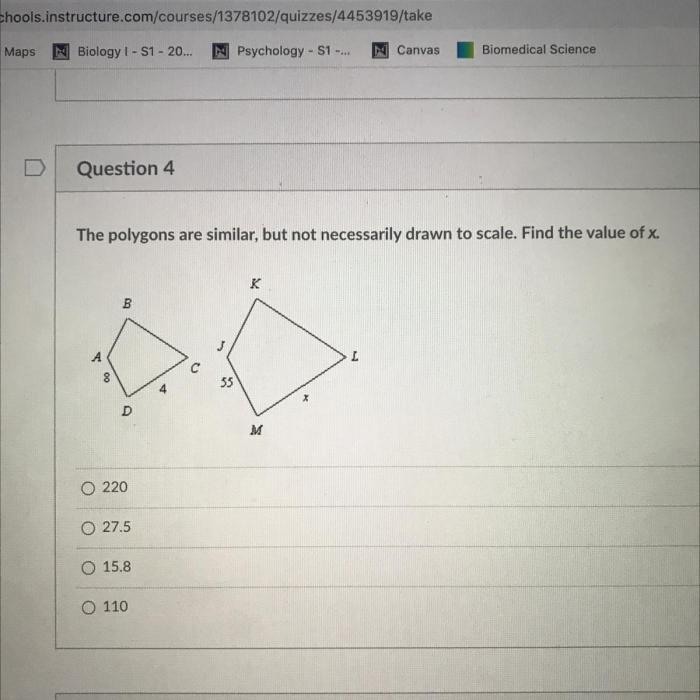
The polygons are similar. find the value of $x$ . – The realm of geometry presents us with fascinating shapes known as polygons, and when these polygons share remarkable similarities, they unveil valuable relationships that can be harnessed to determine unknown values. In this discourse, we delve into the intriguing concept of similar polygons, embarking on a journey to uncover the elusive value of $x$.
Similar polygons grace our world in diverse forms, from the symmetrical petals of a flower to the towering skyscrapers that define our skylines. Their captivating properties, including proportional sides and congruent angles, offer a powerful tool for solving complex geometric problems.
Similar Polygons
Similar polygons are polygons that have the same shape but not necessarily the same size. The corresponding angles of similar polygons are congruent, and the corresponding sides are proportional.
For example, a square and a rectangle are similar polygons because they both have four sides and four right angles. The corresponding sides of a square and a rectangle are proportional, and the corresponding angles are congruent.
Properties of Similar Polygons, The polygons are similar. find the value of $x$ .
- The corresponding angles of similar polygons are congruent.
- The corresponding sides of similar polygons are proportional.
- The ratio of the corresponding sides of similar polygons is called the scale factor.
Finding the Value of x

To find the value of x when given that the polygons are similar, we can use the properties of similar polygons.
For example, let’s say we have a square and a rectangle that are similar. The square has a side length of 5 cm, and the rectangle has a length of 10 cm and a width of 5 cm.
We can use the fact that the corresponding sides of similar polygons are proportional to find the value of x.
The ratio of the corresponding sides of the square and the rectangle is:
5 cm / 10 cm = 1 / 2
This means that the scale factor between the square and the rectangle is 1 / 2.
We can use the scale factor to find the value of x.
The width of the rectangle is 5 cm, and the scale factor is 1 / 2.
This means that the length of the rectangle is 2 – 5 cm = 10 cm.
Proportional Relationships
The corresponding sides and angles of similar polygons are proportional.
For example, let’s say we have a square and a rectangle that are similar. The square has a side length of 5 cm, and the rectangle has a length of 10 cm and a width of 5 cm.
The following table shows the proportional relationships between the corresponding sides and angles of the square and the rectangle:
| Side | Square | Rectangle | Ratio |
|---|---|---|---|
| Length | 5 cm | 10 cm | 1 / 2 |
| Width | 5 cm | 5 cm | 1 / 1 |
| Angle | 90 degrees | 90 degrees | 1 / 1 |
The table shows that the corresponding sides and angles of the square and the rectangle are proportional.
Scale Factor
The scale factor between two similar polygons is the ratio of the corresponding sides.
For example, let’s say we have a square and a rectangle that are similar. The square has a side length of 5 cm, and the rectangle has a length of 10 cm and a width of 5 cm.
The scale factor between the square and the rectangle is:
5 cm / 10 cm = 1 / 2
This means that the square is half the size of the rectangle.
FAQ: The Polygons Are Similar. Find The Value Of $x$ .
What are similar polygons?
Similar polygons are polygons that have the same shape but may differ in size. Their corresponding sides are proportional, and their corresponding angles are congruent.
How do we find the value of $x$ in similar polygons?
To find the value of $x$ in similar polygons, we can use the proportion of corresponding sides. By setting up an equation and solving for $x$, we can determine its unknown value.
What are the applications of finding the value of $x$ in similar polygons?
Finding the value of $x$ in similar polygons has practical applications in various fields, including architecture, engineering, and design. It enables us to determine unknown dimensions, scale models, and solve complex geometric problems.