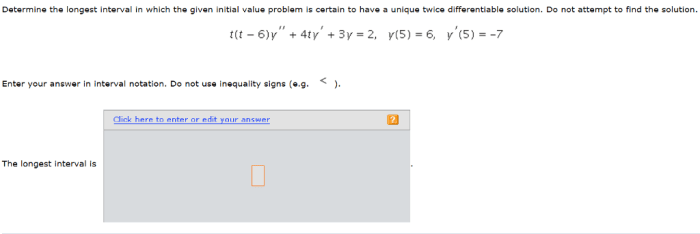
Determine the longest interval in which the initial value problem – In the realm of differential equations, the concept of the longest interval of existence plays a pivotal role in understanding the behavior of solutions to initial value problems (IVPs). This interval defines the temporal domain over which the solution remains valid, offering insights into the dynamics of the underlying system.
By delving into the intricacies of the Picard-Lindelöf theorem, the method of successive approximations, and the significance of Lipschitz conditions, we embark on a journey to unravel the mysteries surrounding the determination of the longest interval of existence.
Initial Value Problem and Longest Interval of Existence: Determine The Longest Interval In Which The Initial Value Problem

An initial value problem (IVP) is a differential equation of the form y’ = f(t, y), together with an initial condition y(t0) = y0. The longest interval of existence for an IVP is the largest interval of time over which a solution to the IVP exists and is unique.
The longest interval of existence is important because it determines the range of validity of the solution to the IVP. If the solution exists and is unique over a longer interval, then we can be more confident in its accuracy.
Methods for Determining the Longest Interval
There are several methods for determining the longest interval of existence for an IVP. One method is the Picard-Lindelöf theorem, which states that if f(t, y) is continuous in a region R and Lipschitz continuous in y, then the IVP has a unique solution that exists and is unique on the largest interval contained in R.
Another method for determining the longest interval of existence is the method of successive approximations. This method involves constructing a sequence of approximations to the solution of the IVP. If the sequence converges, then the limit of the sequence is a solution to the IVP.
The method of successive approximations can be used to determine the longest interval of existence for IVPs that are not Lipschitz continuous in y.
Examples and Applications
The longest interval of existence for an IVP can vary depending on the specific IVP. For example, the IVP y’ = y, y(0) = 1 has a unique solution that exists for all time. However, the IVP y’ = y^2, y(0) = 0 has a unique solution that exists only on the interval (-∞, 0].
The longest interval of existence for an IVP has important implications for the behavior of the solution. For example, if the longest interval of existence is finite, then the solution must eventually become unbounded. This can be useful for understanding the behavior of physical systems, such as the motion of a projectile.
Extensions and Generalizations, Determine the longest interval in which the initial value problem
The concept of the longest interval of existence can be extended to systems of IVPs. A system of IVPs is a set of differential equations of the form y’ = f(t, y), where y is a vector of unknown functions.
The longest interval of existence for a system of IVPs is the largest interval of time over which a unique solution to the system exists.
The concept of the longest interval of existence can also be generalized to non-autonomous IVPs. A non-autonomous IVP is an IVP in which the function f(t, y) depends explicitly on t. The longest interval of existence for a non-autonomous IVP is the largest interval of time over which a unique solution to the IVP exists.
Numerical Methods for Approximating the Longest Interval
There are several numerical methods for approximating the longest interval of existence for an IVP. One method is the Euler method. The Euler method is a first-order numerical method that can be used to approximate the solution to an IVP.
The Euler method can be used to approximate the longest interval of existence for an IVP by increasing the step size until the solution becomes unbounded.
Another method for approximating the longest interval of existence for an IVP is the Runge-Kutta method. The Runge-Kutta method is a higher-order numerical method that can be used to approximate the solution to an IVP. The Runge-Kutta method can be used to approximate the longest interval of existence for an IVP by increasing the order of the method until the solution becomes unbounded.
Key Questions Answered
What is the significance of the longest interval of existence for IVPs?
The longest interval of existence determines the temporal domain over which the solution to an IVP remains valid, providing insights into the behavior of the underlying system.
How does the Picard-Lindelöf theorem contribute to determining the longest interval of existence?
The Picard-Lindelöf theorem establishes conditions under which an IVP has a unique solution that exists and is continuous over an interval containing the initial point.
What role do Lipschitz conditions play in determining the interval of existence?
Lipschitz conditions ensure that the right-hand side of the differential equation satisfies certain smoothness criteria, which play a crucial role in determining the interval of existence for the solution.